Рубрика: Без рубрики

Substitutions in expressions

Any number in the expression can be replaced with the same number, but written in a different form. For example, take the following expression, which has already been calculated:

15 + 3 = 18

Let’s replace the number 15 with the same number, but written in a different form:

(10 + 5) + 3 = 18

You can see that we replaced the number 15 with the expression in brackets (10 + 5). But the main expression 15 + 3 = 18 was not affected by this. Not affected, since 15 and (10 + 5) are the same thing. After all, 10 + 5 = 15.

Let’s replace the number 18 with the same number, but written in a different form:

(10 + 5) + 3 = 3 × 6

Now replace the last number with the same number, but again written in a different form:

(10 + 5) + 3 = 3 × 2 × 3

Now let’s compare two expressions: the first one that we had and the new one that we modified:

15 + 3 = 18

(10 + 5) + 3 = 3 × 2 × 3

At first glance, it seems that these are two different expressions. And so will anyone who sees these two expressions for the first time. But we know that this is the same expression. The only difference is that we changed some of its parameters.

You can change the appearance of this expression indefinitely. The main thing is that equality is not violated. The sign of equality (=) have to justify their position. Remember the second lesson? An equal sign is placed between numbers or expressions only when they are equal.

Such operations, where one number or expression is replaced by itself, but written in a different form, are called conversion or representation.

Representation as a sum

Any number or expression can be represented as a sum. For example, the number 10 can be represented as the sum of 5 + 5 or 7 + 3 or 8 + 2. As long as there is equality between the number and the sum represented. This may look like this:

10 = 5 + 5

10 = 7 + 3

10 = 8 + 2

10 = 6 + 4

In books, you can find the following tasks: present as a sum, and then the numbers or expressions that need to be presented as a sum. This is exactly the case when you need to turn on your creativity and decide which numbers (or expressions) to use to complete the task.

Representation as a difference

From previous lessons, we know that the difference is the result obtained by subtracting one number from another. Difference is also an expression that is connected by a subtraction sign (−). For example the following expressions are differences:

15 – 5

10 – 6

20 – 10

Any number can be represented as a difference. For example, the number 50 can be represented as 90 − 40 or 80 − 30 or 60 − 10. As long as there is equality between the number 50 and the difference represented. It might look like this:

50 = 90 − 40

50 = 80 − 30

50 = 60 − 10

Representation as a work

It is known from previous lessons that a product is a result that is obtained by multiplying one number by another. But a product is also an expression that is connected by a multiplication sign (×). For example the following expressions are multiplying:

3 × 2

15 × 2

12 × 3

Any number can be represented as a product. For example, the number 30 can be represented as a product of 5×6 or 10×3 or 15×2. Whatever you want, as long as the equality between the number 30 and the presented product is observed. This may look like this:

30 = 5 × 6

30 = 10 × 3

30 = 15 × 2

Representation as a private

From previous lessons, we know that a quotient is a result that is obtained by dividing one number by another. But a private expression is also called an expression that is connected by a division sign (÷). For example, the following expressions are private:

15 ÷ 5

30 ÷ 6

12 ÷ 4

Any number can be represented as a quotient. For example, the number 5 can be represented as a quotient of 15 ÷ 3 or 25 ÷ 5 or 30 ÷ 6. As long as there is equality between the number 5 and the quotient represented. This may look like this:

5 = 15 ÷ 3

5 = 25 ÷ 5

5 = 30 ÷ 6

This concludes this lesson. To secure the material, try the following tasks:

Task 1. Present the following numbers as a sum: 20, 30, 45, 50. You can use any number to represent it. For example, the first number 20 can be represented as 15 + 5.

Task 2. Imagine the following numbers as a difference: 10, 15, 12, 5 can be represented by any numbers. For example, the first number can be represented as 15-5.

Task 3. Imagine the following numbers as a multiplication: 30, 40, 72.

Task 4. Present the following numbers as a quotient: 7, 5, 9, 3

Expressions

An expression is any combination of numbers, letters, and operation characters. We can say that all mathematics consists of expressions.

There are two types of expressions: numeric and alphabetic.

Numeric expressions consist of numbers and signs of mathematical operations. For example, the following expressions are numeric:

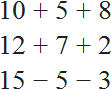
expressions pic 1

Letter expressions contain letters in addition to numbers and operation symbols:

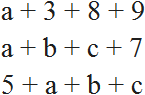
Expressions pic 2

The letters contained in the literal expressions are called variables. Remember this once and for all! Ask any student what a variable is-this question will put him in a stupor, although he can solve complex mathematical problems without knowing what it is. Meanwhile, a variable is a fundamental concept, without understanding which it is impossible to study mathematics.

By the word «study» we mean independent reading of the relevant literature and the ability to understand what is written there. I solve some problems, but I can’t understand what is written in lectures and books. This feeling is familiar to everyone, especially students.

Since the concept of a variable is very important, let’s look at it in more detail. Look carefully at the word «variable». Does this remind you of anything? The word «variable» comes from the words «change», «change your value». A variable in mathematics is always expressed by a letter. For example, write the following expression:

a + 5

This expression. Here is one variable a. since it is a variable, it can change its value at any time. For example, Let’s change the value of this variable. Set it to 5. To do this, write down the variable itself, then put an equal sign and write 5

a = 5

What will happen as a result of this? The value of the variable a, i.e. 5, will be included in the main expression a + 5 and replaced with a.

Expressions pic 3

As a result, we have 5 + 5 = 10.

We have considered the simplest expression. In practice, there are more complex expressions that contain fractions, powers, roots, and parentheses. It looks complicated. In fact, there is nothing complicated about this. The main thing is to understand the principle itself.

In textbooks, the following tasks are often found: find the value of the expression x + 10, for x = 5. Such tasks require that a variable be substituted for its value. Let’s complete this task. The value of the variable x is equal to 5. Substitute this five in the original expression x + 10 and get 5 + 10 = 15.

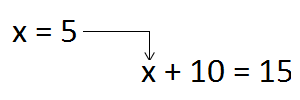
Expressions pic 4

A variable is a kind of container where the value is stored. Variables are convenient because they allow you to prove theorems without giving examples, and write down various formulas and laws.

Remember the second lesson in the «Basic operation». To understand what addition is, we gave the example 5 + 2 = 7, and said that the numbers 5 and 2 are summands, and the number 7 is the sum. But we could understand this topic without an example if we used a literal expression. We would denote the summands with any letters, for example, a and b, and we would denote the sum as c. Then we would get an expression with three variables a + b = c, and we would say that a and b are summands, c is the sum.

And now, having the expression a + b = c, you can use it by substituting any numbers instead of the variables a and b. And the variable c will get its value automatically, depending on which numbers we substitute for a and b

As a practice, you can complete the following task. The expression a + b = c is given. Find its value if a = 10, b = 6. The c variable will get its value automatically. Write the answer as follows: for a = 10 and b = 6, the variable c is equal to such and such a number.

Decision:

a + b = c

10 + 6 = 16

Answer: for a = 10 and b = 6, the variable c is 16.

Expression value

The phrase «perform an action» means to perform one of the actions. In elementary school textbooks, you can often find tasks that contain the following content: «perform an action», and then give examples that need to be solved. When you encounter a similar problem, you should immediately understand that you are required to solve this example. Solving the example and finding the value of the expression is actually the same.

For example, the expression 10 + 6 is given, and we need to find the value of this expression. This means that we have to solve this example. Put an equal sign = and write the answer:

10 + 6 = 16

The resulting sum of 16 is called the value of the expression 10 + 6.

The value of an expression is the result of performing the actions contained in the expression.

Let’s look at a few more examples.:

  • 16 is the value of the expression 4 × 4, since 4 × 4 = 16
  • 20 is the value of the expression 10 + 10, since 10 + 10 = 20
  • 5 is the value of the expression 10 ÷ 2, since 10 ÷ 2 = 5.

Basic operations

The main operations used in mathematics are addition, subtraction, multiplication and division. In addition to these operations, there are also relation operations, such as equal (=), greater than (>), less (<), greater than or equal to (≥), less than or equal to (≤), not equal to (≠).

In general, operations can be divided into two types:
 
  • action actions;
  • relationship operatios.

Action Operations:

addition (+)
subtraction (-)
multiplication (×)
division (÷).

Relationship operations are:

  • equal to ( = )
  • more ( > )
  • less ( < )
  • greater than or equal to ( ≥ )
  • less than or equal to ( ≤ )
  • not equal to ( ≠ ).

Relationship operations

Let’s start with relationship operations. The word “attitude” speaks for itself. Life examples: something has something to do with something. Dad is related to mom. This relationship is called marriage:

step 2 pic 1

There are many examples of relationships. We can say that our beautiful world, which is developing harmoniously, also consists of relationships.

If the five is more than three, then we say that “five is larger with respect to three” and write as 5> 3 (read: five more than three). The acute angle of the sign of the relation should be directed towards the smaller number. In our example, the number 3 was less than the number 5, so the sharp angle of the sign of the relation was directed towards the number 3.

Another example. The number 11 is less than the number 15. This phrase can be written as follows:

11 < 15

In mathematics, relationships can be used to write down laws, formulas, equations, and functions. You can write that one expression is equal to another, or some action is unacceptable in relation to any object, number, law.

For example, the famous phrase «you cannot divide by zero» is written as follows:

step 2 pic 2

We will not get ahead of events and run forward. Just say that you can use any numbers in this expression instead of a and b. But then they say that b should not be zero.

The equal sign = is between the quantities and indicates that these quantities are equal to each other.

For example, “five equals five” is written as 5 = 5. It is clear that two fives are equal to each other. Besides prime numbers, more complex expressions can be combined with an equal sign, for example: 9 + x + y = 4 + 5 + x + y.

Another example: if one large watermelon weighs 20 kg, and two small watermelons weigh 10 kg each, then you can put an equal sign between a watermelon 20 kg and two watermelons of 10 kg. This ratio can be read as follows: «one watermelon weighing 20 kilograms is equal to the weight of two watermelons, each of which weighs 10 kg.» After all, 20 kg = 10 kg + 10 kg.

step 2 pic 3

The sign is not equal ≠ is placed between the quantities when they are not equal to each other.

For example, 5 ≠ 7. It is clear that the five is not equal to the seven. Other examples: a dog is not equal to a cat, mandarin is not an orange:

dog ≠ cat

Mandarin ≠ Orange

You can look around you and find many examples of relationships that can be interpreted from a mathematical point of view.

Addition operation

The addition operation is indicated by a plus sign (+) and is used when adding numbers.

The numbers that add up are called terms. The number that results from their addition is called the sum.

For example, add the numbers 3 and 2.

We write 3 + 2 = 5

In this example, 3 is the term, 2 is the second term, 5 is the sum.

In the future, you will have to add quite large numbers. But the addition of these large numbers will ultimately come down to adding small ones.

Therefore, you need to learn how to add small numbers in the range from 0 to 9. For example:

2 + 2 = 4

3 + 4 = 7

7 + 2 = 9

0 + 7 = 7

You can practice writing a few simple examples in notebooks. Believe me, there is nothing shameful in this.

Subtraction operation

The subtraction operation is indicated by a minus sign (-) and is used when another is subtracted from one number.

The number from which another number is subtracted is called decremented. The number that is subtracted from the decremented number is called subtracted. The number that results is called the difference.

For example, subtract 2 from 10.

10 — 2 = 8

In this example, the number 10 is a decrement, the number 2 is a subtractable, and the number 8 is a difference.

Multiplication operation

It is indicated by a multiplication sign (×) and is used when one number is multiplied by another. The word multiplication speaks for itself — a certain number increases a certain number of times, that is, it multiplies.

For example, a 4 × 3 entry means that the quadruple will be tripled during the multiplication operation.

The number that is increased is called multiplier. A number that shows how many times you need to increase the multiplier is called a factor. The number that results is called the product.

For example, multiply the number 4 by 3.

4 × 3 = 12

In this example, 4 is the multiplicative, 3 is the multiplier, 12 is the product.

The record 4 × 3 can be understood as “repeat the number 4 three times”. For example, if we have four candies and we repeat them three times, then twelve candies come out:

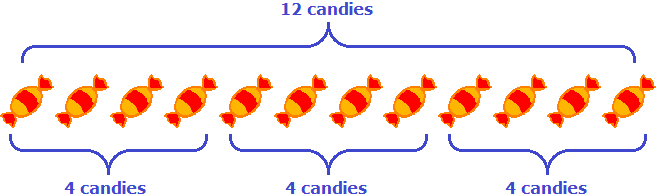
step 2 pic 4

In other words, multiplying 4 by 3 can be represented as the sum of three quadruples. Schematically, it looks like this:

step 2 pic 5

Multiplication can be understood in another way, namely, as taking something a certain number of times. Let’s say candies are in a vase. Take four candies once:

4 conf. × 1 = 4 conf.

We will have four candies in our hands.

Let’s try to take four candies 2 times:

4 conf × 2 = 8 conf

We will have eight candies in our hands.

Let’s try to take four candies zero times, that is, never:

4 × 0 = 0

We won’t have chocolates in our hands, since we never took them. Therefore, multiplying any number by zero gives zero in the answer.

In some books, the multiplier and the multiplier are called by one common word — factors. For example, in a 4 × 3 record, the multiplier is 4, and the factor is 3, but these two numbers can still be called factors. This will not be a mistake.

In the future, we will multiply fairly large numbers. But multiplying large numbers comes down to multiplying small ones. Therefore, you first need to learn how to multiply small numbers. Fortunately, they are already multiplied and recorded in a special table, which is called the multiplication table. You need to know this table by heart:

step 2 pic 6

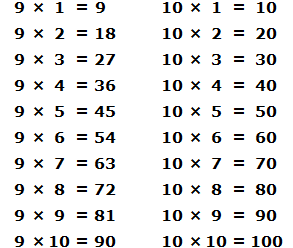
step 2 pic 7

Division operation

The division operation is indicated by a division sign (÷ or 🙂 and is used when dividing numbers.

The number that is divided is called divisible. A number that indicates how many parts the divisible is divided by is called a divisor. The number that results is called a quotient.

For example, divide the number 10 by 2.

10 : 2 = 5

In this example, the number 10 is divisible, the number 2 is a divisor, and the number 5 is a quotient.

If we have ten candies and divide them into two parts, then each part will have five candies:

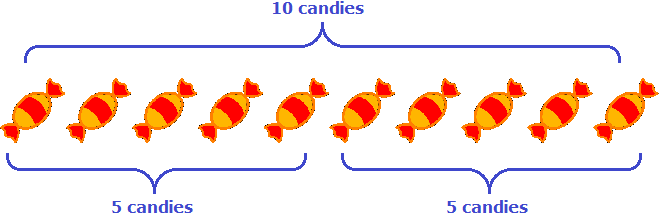
step 2 pic 8

So you can understand the meaning of the entry 10: 2 = 5.

 

The numbers

A number is some entity denoting the number of any objects. Examples: two apples, five spoons, ten books, one hundred rubles, seven tulips. Every day we turn to numbers, sometimes without even noticing it.

At first, when people learned to read and write, the number of subjects was depicted using sticks:

One subject is depicted as |

Two subjects like | |

Three subjects like | | |

Four subjects like | | | |

Five items like | | | | |

When people became more literate, they realized that a large number of objects with sticks could not be represented, and replaced these sticks with numbers.

Today, in mathematics, numbers are denoted by numbers. These are the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. The numbers scare away most schoolchildren and students, as they are associated with mathematics and “scary formulas”. In fact, there is nothing to worry about. Numbers are simply a collection of characters that are intended to represent numbers. Simply put, to indicate the number of items.

That’s all. The introductory lesson on numbers is completed. In the future we will study it much better, but for now, the discussion in this lesson will be enough.